Kleine Quadrätchen – Vorsicht! Arithmetik!!!
Was habe ich mir letztes Jahr um Himmels Willen dabei gedacht, bei den Goodie-Bags von Holst Garn zuzuschlagen? Fünf Tüten mit insgesamt über 600g sind gekommen, in verschiedenen Qualitäten und Farbgruppen, aber nahezu gleicher Lauflänge. Einen Teil der kleinen Knüddelchen von 10-30g habe ich schon mit diversen Resten für ein anderes Projekt vorgesehen, aber 40 Farben, darunter auch etliche Grautöne waren noch vakant.
Die Karenzzeit zwischen Kauf und Nutzung verbrachte ich mit Nachdenken. Sowas soll vorkommen, wenn man ein Projekt plant.
- Erstes Ergebnis war die Überlegung: es sollen kleine gehäkelte Flecken werden.
- Zweiter Gedanke: jeder Flecken soll genau vier Farben beinhalten
- Dritte Idee: regelmäßige Flecken oder verschiedenförmige? Beschluss: beim ersten Projekt dieser Art nur regelmäßige
- Viertes Kriterium: die Flecken sollen sich nicht wiederholen, also: es soll keine zwei gleich aussehende Quadrätchen geben
Ist das möglich? Oder: nach wie vielen Kombinationen wiederholen sich die Patche? Wie hoch ist die Wahrscheinlichkeit, mit 40 Farben zwei identische Patche zu häkeln?
Wir verwenden zur Kalkulation ein paar Rechengesetze. In der Schule tauchte dafür der Begriff “Arithmetik” auf. Da wurde gerechnet und gerechnet und gerechnet, und zwar nur mit ganzen Zahlen.
Das machen wir jetzt auch. Das heißt: ich mache das, ihr könnt einfach nur lesen. Ich hoffe, meine Überlegungen sind plausibel und belegbar. Wer es besser weiß und kann, darf gern korrigieren
Betrachten wir zunächst die Varianten, wenn wir genau vier Farben haben.
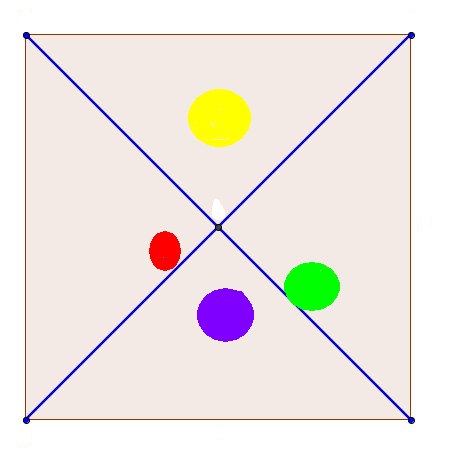
Ich leihe mir rasch ein Quadrat mit Diagonalen, die vier Felder bilden; da kann eine jede nachvollziehen, wie das mit der Belegung für die Positionen aussieht.
Für die erste Farbe haben wir noch vier Positionen zur Auswahl. Wenn diese ihren Platz gefunden hat, gibt es für die nächste Farbe nur noch drei Positionen und so weiter.
Wieviele Möglichkeiten der Anordnung gibt es insgesamt? Hier die Zusammenfassung:
- vier für die erste Farbe
- drei für die zweite
- zwei für die dritte
- eine für die letzte
Demnach haben wir 4*3*2*1 Möglichkeiten vier Farben anzuordnen, das wären 24 Möglichkeiten der Anordnung für vier Farben.
Der 25. Patch, der gehäkelt würde, wäre zwangsläufig ein Zwilling von einem der zuvor gehäkelten Quadrate. Schon erstaunlich, was allein vier Farben hergeben: 24 unterschiedliche Quadrate mit genau vier Farben, ohne, dass eine Farbe mehrfach verwendet wird.
Nun die Überlegung, wie viele verschiedene Patche es gibt, wenn wir fünf Farben zur Auswahl haben?
Die Tüte A enthält fünf Farben und ich nehme vier davon heraus.
- Für die erste Farbe habe ich 5 Zugriffs-Möglichkeiten
- Für die zweite Farbe 4 Zugriffs-Möglichkeiten (denn eine Farbe ist schon draußen)
- Für die dritte Farbe 3 Zugriffs-Möglichkeiten
- Für die vierte Farbe 2 Zugriffs-Möglichkeiten
Demnach habe ich 5*4*3*2 Varianten, also die Möglichkeit, 120 verschiedene Quadrate anzufertigen, das 121ste Quadrat wäre eine Wiederholung eines bereits gehäkelten Quadrates.
Bei sechs verschiedenen Farben wären es 720 unterschiedliche Quadrate, das 721ste wäre eine Wiederkehr eines anderen Eckchens. Um nicht versehentlich ein doppeltes Quadrat zu arbeiten, müsste man Buch führen, mittels einer ausgeklügelten Tabelle. Will das jemand? Vermutlich haben wir das vorerst noch im Blick.
Kommen wir wieder auf die Ausgangsfrage zurück:
Wann tritt wahrscheinlich eine Wiederholung eines Patches bei 40 Farben ein?
Ich nehme vier Farben aus der Tüte A mit 40 Farben
- Für die erste Farbe habe ich 40 Möglichkeiten
- Für die zweite Farbe 39 Möglichkeiten (denn eine Farbe ist schon draußen)
- Für die dritte Farbe 38 Möglichkeiten
- Für die vierte Farbe 37 Möglichkeiten
Demnach habe ich für die vier Farben (ohne festgelegte Reihenfolge oder Anordnung) 40*39*38*37 Varianten, also 2.193.360. Über 2 Millionen Möglichkeiten, aus 40 Farben vierfarbige Eckchen zu fabrizieren: Es ist ziemlich unwahrscheinlich, dass das zweite Quadrätchen genauso aussieht wie das erste, bei einer Wahrscheinlichkeit von 1 zu über zwei Millionen. Das ist immerhin wahrscheinlicher als ein Sechser im Lotto “6 aus 49”, da beträgt die Gewinnwahrscheinlichkeit 1 zu ca. 16 Millionen (ohne Superzahl). Anders ausgedrückt: die Möglichkeit einen Zwilling zu häkeln ist fast siebenmal so hoch als im Lotto zu gewinnen.
Diese 2,2 Millionen Varianten gelten unter der Voraussetzung, dass die Farben/Knäulchen immer wieder in die Tüte A zu den anderen 36 Knäueln zurückgelegt werden, sobald das Quadrat beendet wurde. Wir entnehmen also jedesmal aus der Tüte A mit 40 Farben vier Farben.
Anwendung bei meinem Projekt
Mittlerweile habe ich herausgefunden, dass ich für mein angestrebtes Projekt 130 Quadrate benötige.
Wie hoch ist die Wahrscheinlichkeit, unter diesen 130 Eckchen einen Zwilling zu produzieren?
Um ein wenig Kontrolle darüber zu haben, nicht ständig nach den gleichen Farben zu greifen (meinen Lieblingsfarben zum Beispiel), arbeite ich folgendermaßen:
Ich entnehme der Tüte A zufällig mir in die Hände fallende vier Knäuelchen, häkle den Flecken und lege die abgearbeiteten Farben in eine zweite Tüte B. Das mache ich insgesamt 10mal, dann sind alle Knäuelchen aus Tüte A in Tüte B gewandert. Ich leere diese aus, mische sie gut durcheinander und fülle sie wieder in die Tüte A.
Hier ist die Rechnerei komplexer, aber wir wenden einfach das Bruchrechnen an, wie wir es in der Schule gelernt haben. Nur mit geringfügig höheren Zahlen 😈
Die Überlegungen zur Vorgehensweise lauten:
- die vier Farben, die verwendet wurden, kommen in Tüte B
- daraus ergibt sich, dass man aus 40 Farben 10 verschiedene Patche mit je 24 Varianten häkeln kann, also 240 Möglichkeiten der Gestaltung. Wenn wir nicht Buch führen wollen, wie wir die Farben angeordnet haben, gibt es zehn beliebige, zufällige Patche
- Für jedes der zehn Quadrate berechnen wir die Wahrscheinlichkeit, ab wann ein Quadrat doppelt vorkommt.
- Die einzelnen Wahrscheinlichkeiten für jedes Quadrat müssen wir addieren, um alle Möglichkeiten zu erfassen, also: Wahrscheinlichkeit des ersten Quadrats + Wahrscheinlichkeit des zweiten Quadrats + … + Wahrscheinlichkeit des 13. Quadrats
- Wie wir im Bruchrechnen gelernt haben, ist zum Addieren der Bruchzahlen der Hauptnenner zu ermitteln (mit der Primfaktorzerlegung)
- Nach der Addition und entsprender Quotientenbildung (wie beim Fußball) haben wir dann die Wahrscheinlichkeit, ab welchem Quadrat wir mit dem Zwilling eines zuvor gehäkelten rechnen müssen
1. Berechnung der Wahrscheinlichkeiten für die 10 Patche (siehe Punkt 3 darüber)
| Quadrat | Berechnung der Wahrscheinlichkeit | Wahrscheinlichkeit für das doppelte Patch |
| Patch 1 | 40*39*38*37 | 1 zu 2.193.360, das 2.193.361ste wäre doppelt |
| Patch 2 | 36*35*34*33 (es hat nur noch 36 Farben in der Tüte) | 1 zu 1.413.720 |
| Patch 3 | 32*31*30*29 (es hat nur noch 32 Farben in der Tüte) etc. | 1 zu 863.040 |
| Patch 4 | 28*27*26*25 | 1 zu 491.400 |
| Patch 5 | 24*23*22*21 | 1 zu 255.024 |
| Patch 6 | 20*19*18*17 | 1 zu 116.280 |
| Patch 7 | 16*15*14*13 | 1 zu 43.680 |
| Patch 8 | 12*11*10*9 | 1 zu 11880 |
| Patch 9 | 8*7*6*5 | 1 zu 1680 |
| Patch 10 | 3*3*2*1 | 1 zu 24, das 25ste wäre doppelt |
2. Ermittlung des Hauptnenners als Vorarbeit für Addition (Punkt 5)
Ich habe den Hauptnenner mittels der Primfaktorzerlegung ermittelt: 2^6*3^3*5^2* 7 *11*13*17*19*23*29 *31*37
Leider habe ich keinen Font um Hochzahlen aufzuschreiben, bzw. mathematische Zeichen zu verwenden. Als ausgeschriebene Zahl sieht der Hauptnenner so aus: 1.068.586.291.4126.400, so ähnlich wie die Höhe der Staatsverschuldung eines mittelamerikanischen Kleinstaates.
Den Wert habe ich händisch berechnet, denn Excel ist bei der Hauptnennersuche ausgestiegen, mit neun Werten ging es noch, beim zehnten hat Excel die Grätsche gemacht. Einen Rechenfehler will ich nicht ausschließen.
Damit kann ich die geplante Vorgehensweise, die Wahrscheinlichkeiten der 10 gearbeiteten Patche auf den Hauptnenner zu bringen, knicken. Oder ehrlicher: das ist mir dann doch zu mühsam. Diese Prozedur mitzuverfolgen bleibt der werten Leserschaft dann auch erspart.
Da mich die Fragestellung doch fasziniert, nehme ich nur zwei Werte, nämlich die beiden mittleren von den 10 Quadrätchen, die Wahrscheinlichkeiten von 1 zu 255.024 und 1 zu 116.280, beim fünften und sechsten Quadrat. Meine Überlegung ist: bei den ersten Quadraten ist die Wahrscheinlichkeit niedriger, ein Doppeltes zu häkeln, bei den letzten höher, das ist trivial, dafür braucht man nur auf die Wahrscheinlichkeiten zu schauen und benötigt dazu keine Arithmetik.
Gleiches Vorgehen:
- Hauptnenner der beiden Wahrscheinlichkeiten suchen, der ist 411.863.760
- bei beiden Wahrscheinlichkeiten die Zähler erweitern und addieren: das wären 3542 + 1615 = 5157
- Die Wahrscheinlichkeit wäre dann, ohlala: 1/79865
Das bedeutet: es ist mit einer Wahrscheinlichkeit von ca. 1 zu 80.000 damit rechnen, ein doppeltes Quadrat zu erzeugen. Da kann man drum herum kommen, indem man rasch einen Blick auf die bisher gehäkelten Quadrätchen wirft.
Da ich das Procedere für 130 Patche 13mal durchführe, beträgt die Wahrscheinlichkeit 13 zu 79865 oder 1 zu 6144. Klar ausgedrückt: je häufiger ich nach der vorgestellten Methode (mit Weglegen der benutzten Farben) zehn Quadrate häkle, umso höher wird die Wahrscheinlichkeit, dass auch mal zwei gleiche dabei sind.
Und es ist dennoch eine hypothetische Ermittlung. Uns wurde von Kernkraftbetreibern auch seit Jahrzehnten immer wieder versichert, ein schweres Kraftwerkunglück passiere nur mit der Wahrscheinlichkeit von einem in 10.000 Jahren. Dennoch hatten wir Tschernobyl und Fukushima schon innerhalb von nichtmal 30 Jahren. Von weiteren Ereignissen, die nicht unmittelbar menschheitsgefährdend sind, ganz abgesehen. Kernkraftwerkbetreiber müssten im Grunde diese Ereignisse nehmen, um neue Berechnungen durchzuführen, oder?
So ist es dann auch bei der Berechnung der Wahrscheinlichkeit des doppelten Quadrats: das Vorkommen der Verdopplung nach 6144 Quadraten erscheint recht sicher. Wenn man über die Verteilung genau Buch führt, kann man 6144 Quadrate anfertigen, das 6145ste ist dann ein doppeltes eines vorangehäkelten. Wenn man ohne Buchführung arbeitet, kann es auch bereits das 16. Quadrat sein, das schon einmal vorgekommen ist.
Analog kann man für das Lottospielen argumentieren: bei einer Wahrscheinlichkeit von 1 zu ca. 16 Millionen für einen Sechser ohne Zusatzzahl kann man nicht voraussagen, ob man gewinnt, wenn man seinen ersten Lottoschein abgibt oder den 5000sten.
Ich könnte also behaupten: ich weiß genau, dass meine Lottozahlen mal gezogen werden, ich weiß nur nicht genau, wann.
Was ein echter Mathematiker dazu schreibt
Er sagt: innerhalb des ersten 10er-Durchgangs kann es keine zwei gleichen Quadrate geben, also brauchte man nur die Wahrscheinlichkeiten für die Durchgänge 2 bis 13 zu berechnen. Aha: deshalb sind die Rechner vermutlich ausgestiegen, weil ich diese Wahrscheinlichkeit immer mit reingenommen habe.
Seine Rechnungen sehen ähnlich komplex aus wie meine und auch hier steigt der Rechner aus. Der Mathematiker hat das ebenfalls festgestellt und schreibt, dass die Berechnungen sehr mühselig seien. Wie wahr!
Eine seiner Aussagen muss ich noch dahingehend überprüfen, ob es Auswirkungen auf meine berechneten Wahrscheinlichkeiten hat. Oberflächlich habe ich einmal gerechnet, es ändert sich eine Zahl, die jedoch für die Praxis keine wesentliche Auswirkung hat, wenn ich mit Buchführung häkle, benötigt es immer noch ein paar Tausend Quadrätchen bis zur ersten Verdopplung, und wenn ich nach dem Zufallsprinzip häkle, kann das gleiche passieren, wie beim Kernkraftwerk.
Vielen Dank, Manni, F., an deinen Ausführungen habe ich großes Vergnügen und werde eventuell noch einmal darauf zurück kommen.
Und was soll das Ganze? Warum mache ich die ganze Rechnerei?
- ich hätte das Projekt gerne schon vorgestellt, es geht aber nicht so schnell voran, wie ich dachte, diese Ausführungen dienen der Überbrückung. Klar: in der Zeit, in der ich hier herumgerechnet und den Blogbeitrag geschrieben habe, hätte ich ebensogut 5-6 Quadrate häkeln können, mindestens. Seit Beginn des Monats handarbeite ich an nichts anderem und es macht einen Heidenspaß.
- mich fasziniert, wie man scheinbar zufällige, auf den ersten Blick nicht steuerbare Ereignisse mathematisch berechnen kann. Wenn etwas verlässlich ist, dann ist es die Mathematik. Das ist doch beruhigend.
Was geschieht eigentlich mit den Häkelflecken? Es soll daraus ein Zierschal in einem ganz bestimmten Stil werden. Über die Art des Designs wird dann bei Fertigstellung des Projekts berichtet.
Wer nun glaubt, ich sei die einzige Irre, die sich über den mathematischen Hintergrund von Gestricktem oder Gehäkeltem Gedanken macht, hat sich getäuscht.
Wer weiter lesen will, hier ein paar Beispiele
http://geekknitting.blogspot.com/
http://www.woollythoughts.com/aboutus.html
http://www.toroidalsnark.net/mathknit.html
http://komplexify.com/blog/2007/06/09/bedspread-mathematics/

Ich kenne mich ja mit Häkeln nicht ganz so gut aus…. aber da gibt es eine definierte Vorder- und Rückseite, oder? Denn mit kraus-rechts-Quadraten hätte deine Rechnerei etwas anders ausgesehen. denn da hättest du mehr Dopplungen gehabt, weil das Wenden dir einige Farbverteilungen “gleich macht”
soweit mein Senf 😉
Ich finde es faszinierend, was du dir immer überlegst!!!!
In der Tat: vorn und hinten sind unterscheidbar, wobei die Rückseite dieses Musters ganz passabel aussieht.
Bei krausrechts sieht man auch, was “hinten” ist. Für die Auswahl der Farben und der Anordnung spielen Vorder- und Rückseite jedoch keine Rolle.
Für kalkulatorische Berechnungen werden daher vermutlich immer Kugeln genommen, weil es damit keine Vorder- und Rückseiten gibt.
Im Moment bin ich dabei, die restlichen Fäden zu vernähen: morgen könnte das Werk vollendet sein. Der Bericht ist schon geschrieben, es fehlen noch die Bilder. Damit ist das Strickstück meine einzige Fertigstellung im Oktober.
“Die Karenzzeit zwischen Kauf und Nutzung verbrachte ich mit Nachdenken. Sowas soll vorkommen, wenn man ein Projekt plant.”
Klasse!!
Ja, sowas soll tatsächlich vorkommen : )
Ich rechne bei Projektplanungen auch, allerdings nicht ganz so komplex wie Du.
Ich glaube, bei Deiner Fragestellung würde ich einen pragmatischeren Ansatz verfolgen:
Beliebige Farbe A aus der Tüte nehmen, in – sagen wir mal 4-5, über die genaue Zahl müsste ich nachdenken und rechnen, was ich v.a. nachts gut kann – Patches mit beliebigen Farbkombinationen verarbeiten, dann Farbe A aus dem Verkehr ziehen. Wenn Farbe A nicht mehr auftaucht, gibt es auch kein zufällig gleiches Patch mehr, Wahrscheinlichkeit hin oder her.
Mit Farbe B ebenso verfahren usw…
Viel Spaß beim Häkeln!
LG Hummelbrummel
Vielen Dank, liebe Hummelbrummel,
Das stimmt: wenn man die Farbe rauslegt, ist sie auch nicht mehr nutzbar. Das war auch eine meiner Überlegungen. Das wäre eine Methode ohne Zufallsprinzip, also mit zumindest teilweiser Buchführung.
Allerdings: für eine Verteilung gibt es dann die Überlegung: mit welche Farben zusammen soll die Farbe A eingesetzt werden: zufällig oder gewählt?
Man erkennt: da gibt es wieder viele (berechenbare) Möglichkeiten.
Mein Ziel war zu berechnen: tritt der Fall des doppelten Patches schnell ein oder wann muss man damit rechnen?
Wenn ich Häkeln mit Buchführung mache, also nichts dem Zufall überlasse: wie viele Möglichkeiten muss ich aufschreiben? Es gibt ja schon für eine einzige Farbe Tausende von Varianten, und die praktische Umsetzung wäre eine Strafe für jemanden, der Vater und Mutter ermordet hat.
Mit der Entnahme “vier aus 40, 36, 32 …” habe ich schon eine kleine Steuerung übernommen, aber immer noch jede Menge Zufall.
Mir kommen solche Ideen auch immer nachts, bzw. sie können sehr hilfreich beim Einschlafen sein 🙂
Ich hatte sogar schon ein kleines Excel-Programm angedacht, das mir auf Tastendruck eine Zufallsverteilung ausspuckt, programmtechnisch kein großer Akt, ich müsste mich in sowas nur wieder einarbeiten.
Aber das ist es dann doch nicht Wert, lieber will ich das Projekt bald beendet haben.
Soll ein Geschenk werden …