Parkett und Parkettierung
Als ich eine großzügige Wollspende von Susn ordnete, fanden sich fünf Knäuel “Katia Darling” (keine Werbung, sondern Markennennung zwecks Kennzeichnung). Die Farbvariante des Verlaufsgarns kann man gut als “herbstlich” bezeichnen. Fünf Knäule sind bei der Deckenproduktion eine Füllung für den hohlen Zahn. Allerdings wollten diese bunten Bällchen nicht in einer Riesendecke verschwinden, sondern gerierten sich eitel. Also gut: dann eben eine Extrawurst.
Da bietet sich für die geplante Babydecke das Baukastenprinzip von Horst Schulz an. Die Horst Schulz’sche Modultechnik basiert auf der Parkettierung. Über Horst Schulz wurde bereits verschiedentlich berichtet.
Parkettierung ist ein Teilbereich der Geometrie, als mathematisches Phänomen taucht es bereits bei Euklid auf, der ca. im 3. Jahrhundert vor Christus lebte. Euklid bescherte uns nicht nur mathematische Erkenntnisse geometrischer Art, sondern ist auch in der Musiktheorie bedeutsam. Er schrieb die älteste überlieferte Darstellung eines Tonsystems am Beispiel des Kanons.
Wir bleiben jedoch bei der Parkettierung, die es demnach viel früher gab, als das Parkett, unter dem sich vermutlich die meisten den Bodenbelag aus Holz oder künstlichen Werkstoffen vorstellen. Parkettierung umschließt auch die Kachelung oder Pflasterung und strebt an, aus möglichst einfachen Formen eine Fläche abzudecken, ohne Überstände oder Reste. Mit Kreisen ist demnach keine Parkettierung im euklidischen oder platonischen Sinn möglich, nur mit Vielecken.
Ein Meister der Parkettierung in zeichnerischer oder holzschnitzender Form war der niederländische Grafiker und Künstler Maurits Cornelis Escher. Seine Berühmtheit basiert nicht nur auf der Brillanz seiner Zeichenkunst, sondern, weil er das Thema Parkettierung vor allem mit ungewöhnlichen Formen aufgriff.


Nun hat M.C. Escher nicht einfach ein wenig herumprobiert und passend gemacht, sondern die Escher-Parkette basieren auf mathematischen Grundlagen, den Laves-Netzen.
Ein wenig Geometrie will ich euch jetzt nicht ersparen, weil hier eine interessante Begegnung stattfindet.
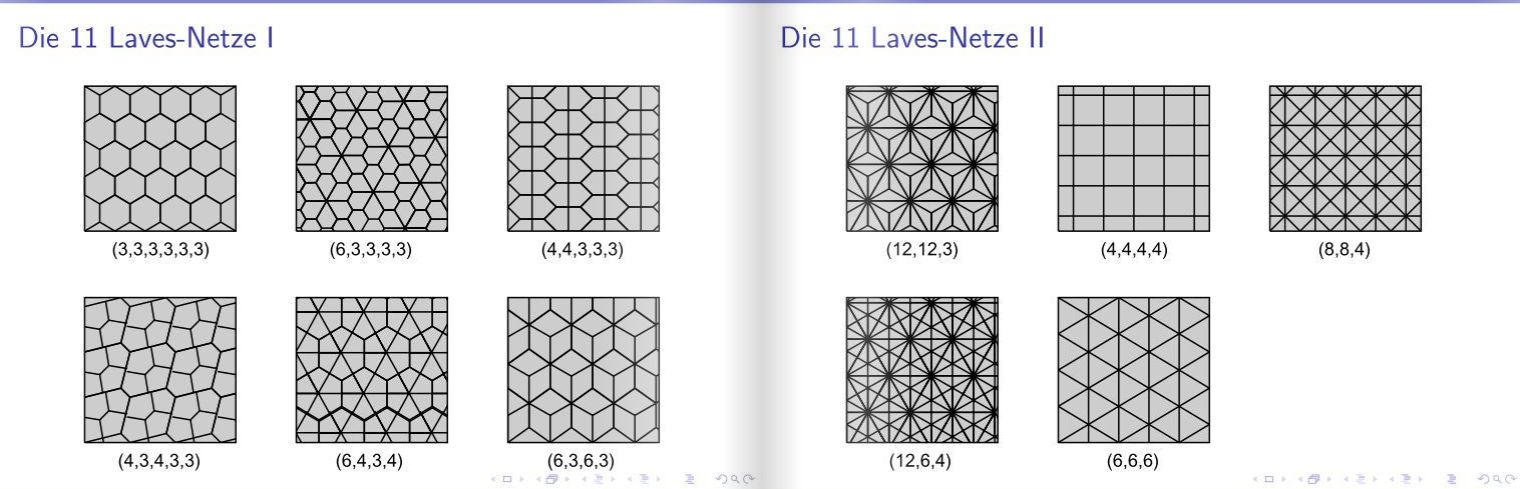
1931 bestimmte Fritz Laves – er war gerade 26 Jahre alt – die elf homogenen Netze der Ebene (auch Laves-Netze). Dabei handelt es sich um die Parkettierung der Ebene durch endlich viele gleiche oder spiegelbildlich gleiche Polygone, also Vielecke, wobei jedes Polygon von der Gesamtheit der anderen in gleicher oder spiegelbildlich gleicher Weise umgeben ist. Das hört sich ausgesprochen abstrakt an, daher ein Bild der Netze, entnommen dem Magazin “Escher-Parkettierungen” von Manfred Dobrowolski, Universität Würzburg (siehe unten).
Escher war acht Jahre älter als Laves. Die Escher-Parkette tauchen ab ca. 1935 verstärkt auf. Gut möglich, dass Escher Laves’ Erkenntnisse aufgriff und als Elemente für seine Parkette nutzte.
Die Escher-Parkette sind jedoch durch eine spezielle Definition gekennzeichnet: Ein Escher-Parkett ist ein Laves-Netz, in dem es keine geraden Kanten und keine Spiegelsymmetrien gibt. Diese Klassifizierung stammt von Heinrich Heesch, ein Mathematiker mit dem Schwerpunkt Geometrie und ebenfalls ein Zeitgenosse von Escher und Laves. Er hat 28 Arten von Escher-Parketten herausgearbeitet, basierend auf Drei-/Vier-/Fünf- und Sechsecken.
Wenn wir uns oben das Bild mit den orange und grünen Echsen ansehen, erkennen wir feine Linien, die zeigen, dass auf der Basis von Quadraten gearbeitet wird. Möglicherweise ein Holzschnitt, mit dem er fortlaufend parkettiert hat, ich habe es nicht recherchiert.
Im SPIEGEL-Artikel “Vom Quadrat zur Vogelkachel” sehen wir, wie ein Parkett entsteht. Wobei es kein Escher-Parkett gemäß der o.g. Definition ist, da es über gerade Kanten verfügt. Dafür ist die Darstellung sehr hilfreich und anschaulich.
Verschiedentlich gibt es Aktivitäten, Eschers Kunst in Strick abzubilden. Jana Huck hat sich mit diesen Designs der ausgesprochen erfolgreichen Umsetzung gewidmet. Urheberschaft der Abbildungen: Jana Huck.
 |  |
Nachdem wir ambitionierte Parkettierungen betrachtet haben, geht es zurück zu einfacherer Formgebung.
Eine nette Idee zum Häkeln ist diese Decke aus Kätzchenparkett. Das kostenlose Muster von Sandra Miller Maxfield kann man von hier downloaden.
Das Foto stammt ebenfalls von der genannten Website.
“Meine” Parkettierung ist noch einfacher und besteht lediglich aus Quadraten und langgezogenenSechsecken.
Schaut man sich die Grundlage für das Parkett an, erkennt man: die Einteilung der Kachel, die immer wieder angelegt wird, besteht aus vier Trapezen um ein Quadrat gruppiert.
Ob Horst Schulz diese Art der Parkettierung je genutzt hat, ist mir nicht bekannt, ich nutze lediglich seine Technik des Aneinanderstrickens.
Ich habe das Parkett schnell auf ein Karopapier gezeichnet und die Reihenfolge notiert.

| 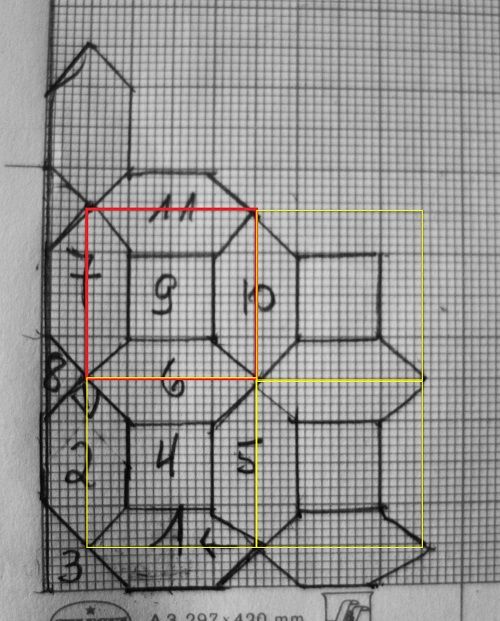
|
Wenn ich geometrisch noch einen draufsetzen will, kann ich sagen: Das Parkett mit meiner Kachel ist sowohl spiegel- als auch drehsymmetrisch.
Ich geh dann mal kacheln.


Hallo,
ich bin heute zum ersten Mal auf Deinen Seiten gelandet und total begeistert. Ich stricke hauptsächlich, manchmal häkele ich auch. Neben der Faszination fürs Handarbeiten und Selbermachen an sich gefallen mir vor allem diese mathematischen Überlegungen. Da bin ich ja bei Dir absolut richtig! Die Parkettierung muss ich mir mal durch den Kopf gehen lassen. Würde ja auch für Pulli-Muster funktionieren…
Danke für die tollen Inspirationen und die Hintergrund-Infos! Hab einen schönen Tag
Vielen Dank, liebe Moni!
Ja, das Parkettieren funktioniert auch bei Pullis, lass es mich wissen, wenn du so etwas planst.
Gleich veröffentliche ich das Ergebnis der theoretischen Vorüberlegungen.
Liebe Grüße
Michaela